2
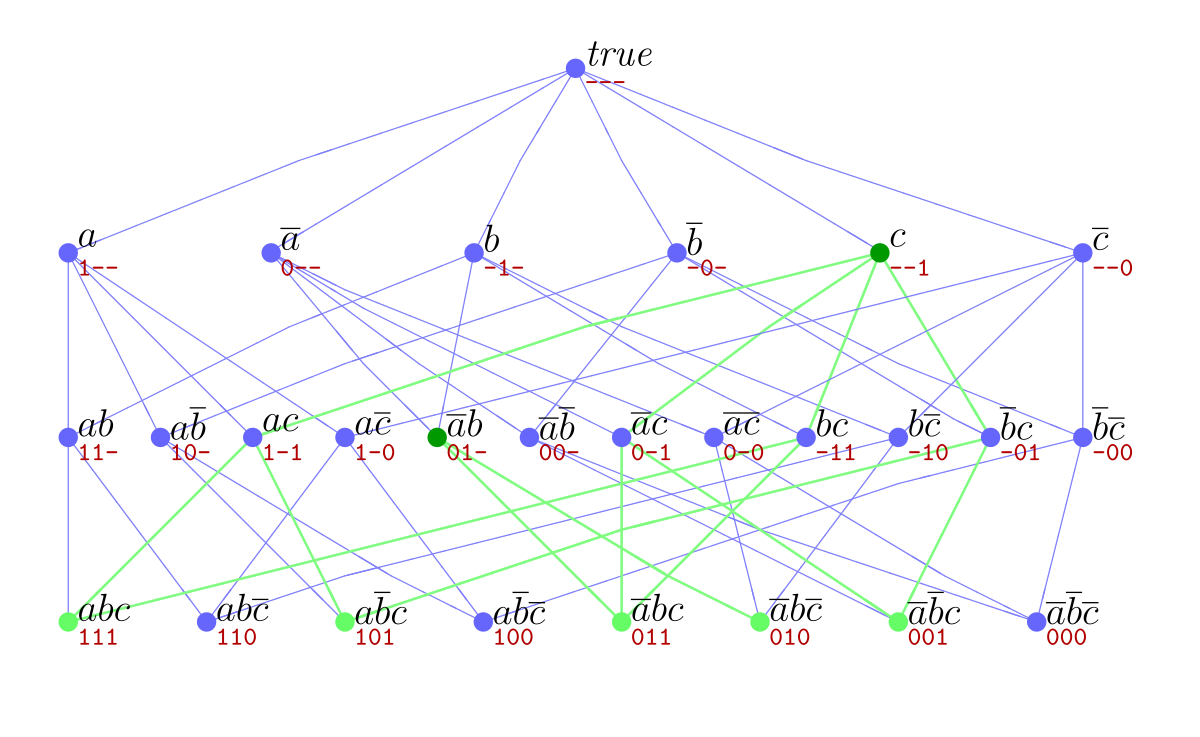
If #abc=0#, #abbcca=2# and #abc=1# then what is the value of #a^2/(bc) b^2/(ca) c^2/(ab)# ?If a b c 0 and a 2 b 2 c 2 16 find the value of ab bc ca Tutorix
Ab+bc+ca=0 find the value of
Ab+bc+ca=0 find the value of-By the AMGM inequality, $\displaystyle xy\le\frac{x^2y^2}{2}\;$ So we have $\displaystyle\begin{align} abbcca &\le \left(\frac{a^2b^2}{2}\right)\left(\frac{b^2C $001 C $15 shipping C $15 shipping C $15 shipping CKStamps Powerful Mint Russia Stamps & Sheets Collection In 2 Binders, Most NH US High Value
26 1f Ab Ca 0 Find The Value Of A 2 B C Hint Ab Ca T Ca Ca A Ab C C C C 27 Find The Value Of X 2a 3 X 3b 3 X C 3 3 X 2a X 3b X C When 3x
Find many great new & used options and get the best deals for CKStamps Useful Mint & Used Russia Stamps & Covers Collection In 2 Volumes at the best online prices at eBay! If a b c = 9 and ab bc ca = 23, find the value of a2 b2 c2 by tony#shark LearnyVerse Wizard (743k points) asked in Maths 9th 0 votes If the roots ff the equation (c2 – ab)x2 – 2(a2 – bc)x b2 – ac = 0 are equal, then prove that either a = 0 or a3 b3 c3 = 3abc by God_Of_FreeFire Centurio General (NCERT Solutions For Class 12 Chemistry;
If ab bc ca=0 then find the value of 1 ÷(abc)1÷(bbca) 1÷(ccab) Ask questions, doubts, problems and we will help you If ab bc ca=0 then find the value of 1 ÷(abc)1÷(bbca) 1÷(ccab) Report ;$\begingroup$ what i intended was that suppose that abc=k(come constant), then the maximum value of abc occurs when a=b=c this is similar when we consider a parallelogram with constant perimeter given the one with the highest area is alwaysIf abbcca=0, then the value of a 2−bc1 b 2−ca1 c 2−ab1 will be A −1 B abc C abc D 0 Medium Solution Verified by Toppr Correct option is D) abbcca=0 bc=−ca−ab bc=−a(bc)eq1 like wise, ab=−c(ab)eq2 & ca=−b(ca)eq3 = a 2−bc1 b 2−ca1 c 2−ab1 taking the value from eq1, 2&3 = a 2a(bc)1 b 2b(ac)1 c 2c(ab)1
Ab+bc+ca=0 find the value ofのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
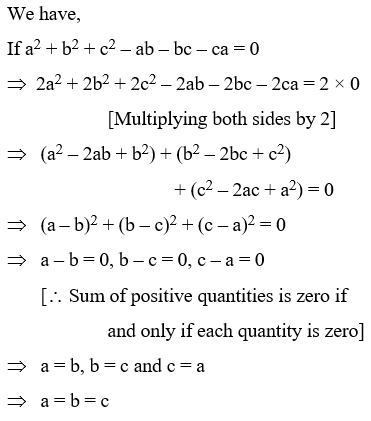 |  | |
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
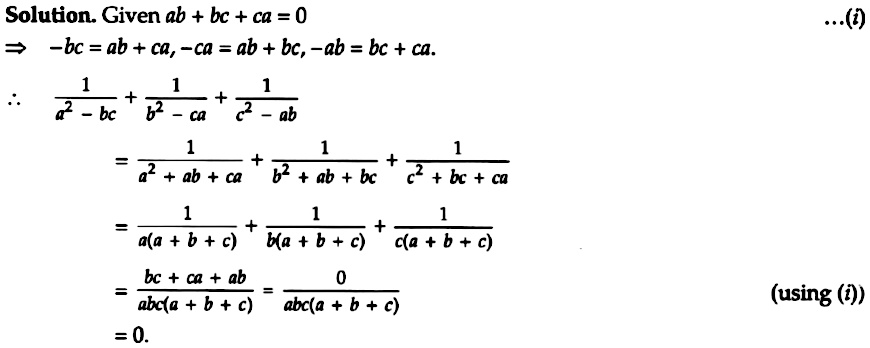 |  |  |
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 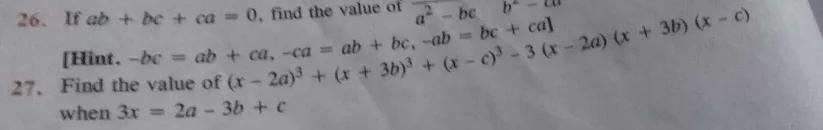 |
 | ||
 |  |  |
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
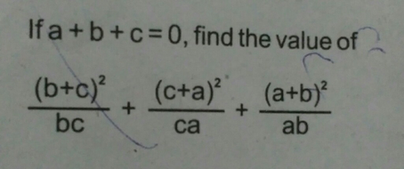 |  |  |
 |  | |
 |  |  |
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
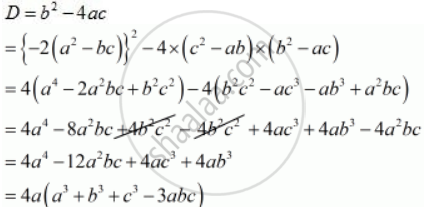 |  | |
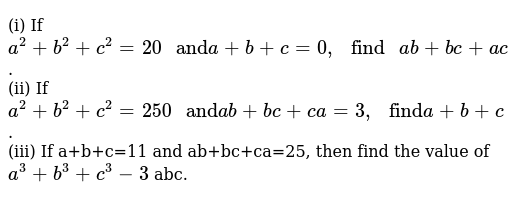 |  |  |
「Ab+bc+ca=0 find the value of」の画像ギャラリー、詳細は各画像をクリックしてください。
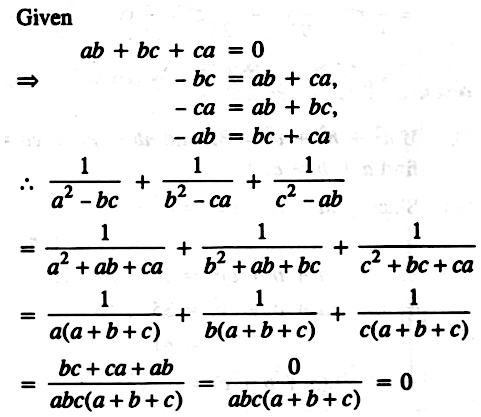 |  | |
 |  |  |
Setting each to $0$, we get that $$\lambda = \frac{1ab}{ab} = \frac{1ac}{ac} = \frac{1bc}{bc}$$ in addition to our original constraint Expanding $\frac{1ab}{ab} = \frac{1ac}{ac}$ yields that $$aca^2babc = aba^2cabc$$ $$(a^21)b = (a^21)c$$ $$a=\pm 1\mathrm{\ or\ } b=c$$ Since $0When a b c = 0 Given then, a 3 b 3 c 3 = 3 a b c ⇒ a 3 a b c b 3 a b c c 3 a b c = 3 On dividing a b c both sides ⇒ a 2 b c b 2 a c c 2 a b = 3
Incoming Term: ab+bc+ca=0 find the value of,




0 件のコメント:
コメントを投稿